Noah Kent
Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA, USA
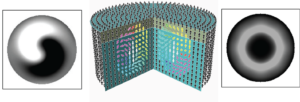
Hopfions are topological structures defined by a Hopf charge, Q [1]. Q is the number of times every field line in order parameter space wraps around each other. To clearly talk about three dimensional magnetic Hopfions and their possible future uses, I will first discuss topological mappings, why topologically protected three dimensional Skyrmions can’t exist in ferromagnetic systems [2], and give an overview of the various types of 3D Hopfions (e.g. Skyrmion tube, heliknoton [3]).
I will then talk about the experimental realization of magnetic Hopfions [4], and how they were identified by differentiating them from other possible magnetic structures using a combination of depth averaging magnetic transmission x-ray microscopy and surface sensitive photo-emission electron microscopy.
Finally, I will discuss why Hopfions have significant technological potential (e.g. unique interactivity, multiple structurally distinct hopfions for a given Q) and give a brief outline of future experimental goals that must be reached in order to realize this potential.
Reference(s)
[1] Nicholas Manton, Paul Sutcliffe, Topological Solitons, Cambridge University Press. 2004
[2] H.B. Braun, Topological effects in nanomagnetism: from superparamagnetism to chiral quantum solitons, Advances in Physics (2012).
[3] Tai J-SB, Smalyukh II. Three-dimensional crystals of adaptive knots. Science. 2019;365:1449–1453.
[4] Kent, N., Reynolds, N., Raftrey, D. et al. Creation and observation of Hopfions in magnetic multilayer systems. Nat Commun 12, 1562 (2021). https://doi.org/10.1038